核磁共振

碳十三核磁共振光譜

★前言

國內目前最大的新聞之一是「核四是否續建」，那是利用核分裂產生能量來發電，這回介紹的主題和原子核有關，不過不是鈾的原子核，而是碳十三同位素。

「核磁共振」的「核」是指原子核，「磁」是指磁場，原子核在磁場和無線電波的作用之下產生能量共振的現象稱為核磁共振。這個現象在1940年代之前就被科學家所發現，在1965年以前就有簡單的數學式可以預測「化學位移」的數值。

「化學位移」是碳十三核磁共振光譜提供的重要訊息之一，它告訴我們碳原子在分子結構中所處的環境，而碳是天然物結構組成裡最多的原子，得知碳所處的環境，對於結構的解析相當重要。

★測驗

好了！舉例吧！先來個簡單的測驗，挑戰您對碳十三光譜的理解程度。

1.	正庚烷有七個碳，請問每個碳的化學位移數值是多少？「可惡，查書不就知道了嗎？誰那麼無聊去背這個啊！」「別生氣，放輕鬆！夠熟悉的話，這是常識，而且也有知識可以預測喔！別急，待會兒會告訴你。」
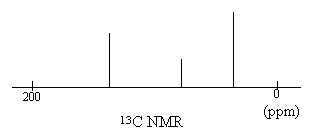
2.	正庚烷雖有七個碳，碳十三核磁共振光譜只有四個訊號，化學位移分別是32.6, 29.7, 23.2,及14.1 (ppm)，請問各是那個碳的訊號？[ppm 是化學位移的單位，和濃度單位的ppm有不同的意義。]
3.	解光譜：碳十三光譜資料 38.98, 34.17, 29.55, 20.18, 19.20, 14.40, 11.43，分子式C₇H₁₆，求解結構式。

★碳十三化學位移計算器

有困難嗎？如果有的話，提供一個計算器給您，上面三個問題都適用，只要輸入正確的參數，就可以得到化學位移的近似值。在此先做些簡單的說明：（您也可以不看以下說明，直接按鈕打開計算器視窗。

★解析環境變數

前面提過，化學位移受所處環境影響，因此要輸入的參數正是一些環境變數，例如和所要計算的碳相隔幾個化學鍵，以及相鄰碳的種類。

假定把要計算化學位移的碳稱為目標碳的話，則

和目標碳相隔一個化學鍵的碳稱為α碳；
和目標碳相隔兩個化學鍵的碳稱為β碳；
和目標碳相隔三個化學鍵的碳稱為γ碳；
和目標碳相隔四個化學鍵的碳稱為δ碳；
和目標碳相隔五個化學鍵的碳稱為ε碳；

首先要設定的是上述五種碳的個數，這可在計算器選單上點選完成。

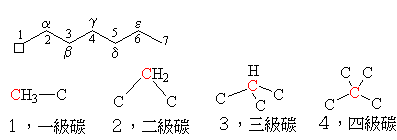
碳有四個化學鍵可和其他原子相接，所接的原子可以是氫，可以是碳，也可以是氧、硫、矽、氟…等其他原子，一個碳原子週邊的碳原子數目稱為那個碳的級數：

只和一個碳原子相鄰的碳稱為一級碳，在此以１表示；
和兩個碳原子相鄰的碳稱為二級碳，在此以２表示；
和三個碳原子相鄰的碳稱為三級碳，在此以３表示；
和四個碳原子相鄰的碳稱為四級碳，在此以４表示；

各級碳的數目是接下來要設定的，也可在計算器選單上點選。

圖示：（假定目標碳為正庚烷的一號碳）

表一、正庚烷各類型碳的分析結果
(碳四的部份請自行填入，當作練習)


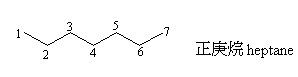變數	α	β	γ	δ	ε	１	２	３	４	預估	計算1	計算2	實際
C1C7	1	1	1	1	1	0	1	0	0	13	13.9	13.86	14.1
C2C6	2	1	1	1	1	1	1	0	0	22	23.0	22.65	23.2
C3C6	2	2	1	1	0	0	2	0	0	31	32.3	32.40	32.6
C4

★從環境變數預估化學位移

仔細把上表看一看，不難發現各個碳所處環境的異同。預測各個碳的化學位移也不難，粗略地算法是把α碳和β碳的數目相加之後乘以九，再把γ碳的數目加1之後乘以(-2.5)，最後再把兩個相乘的結果加在一起，所得的數值就是化學位移的粗略估計值，您不妨先用這個方法估計一下正庚烷中每個碳的化學位移數值大約範圍。這裡以碳二為例來算一算：
碳二有兩個α碳，一個β碳，一個γ碳，所以是 (2+1)x9 + (1+1)x(-2.5) = 27-5=22。

理解之後，可先估計其他碳化學位移的約略範圍，碳一約是13 [(1+1)x9+(1+1)x(-2.5)]，碳三約31 [(2+2)x9+(1+1)x(-2.5)]，碳四約29 [(2+2)x9+(2+1)x(-2.5)]，碳五同碳三，碳六同碳二，碳七同碳一，這些數值和第二題給的蠻接近的([31,29,22,13]對[32.6, 29.7, 23.2,14.1])，這樣已足以推定碳一和碳七的化學位移為14.1 ppm，碳二/碳六為23.2，碳三/碳五為32.6，碳四為29.7。您也可回到上頭按鈕開啟計算器視窗，算出更接近的數值，也可玩一玩站長努力寫的小程式。(結果已列在表一)
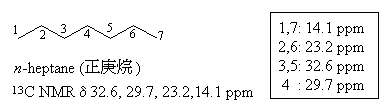
1、2題解答

★小結

上圖是第一題及第二題的答案，碳二碳三碳四同為二級碳，化學位移相差很大，其結果是否出乎您的意料呢？前面已解釋了部份理由，「化學位移受環境影響」，其中最主要的影響因素是αβγ三種碳的個數，α和β碳會增加目標碳的化學位移值，γ碳則會使目標碳化學位移值減小。碳三比碳二多一個β碳，故化學位移值較大，碳四和碳三的β碳數目相同，但卻多了個γ碳，所以化學位移比碳二大，卻比碳三小。

★挑戰第三題

第三題解出來了沒？這題較複雜，得具備基本的有機化學常識，例如對異構物的認識。

單憑碳十三化學位移數據並不足以推導出整個分子的結構，有分子式的話，問題就簡單多了。而目前的光譜技術可在得到碳化學位移之外也得到碳的級數，因此第三題可分成兩個層次來探討。首先考慮只有碳譜及分子式的情形，其次把DEPT資訊加入。

C₇H₁₆可能是正庚烷 (A)；可能是接了一個甲基的正己烷(7=6+1)(B,C)；可能是接了兩個甲基的正戊烷(7=5+1+1)(D,E,F,G)，或者不是兩個甲基，而是一個乙基(7=5+2)(H)；此外還有4+1+1+1的可能(I)。列出所有的可能結構。
異構物

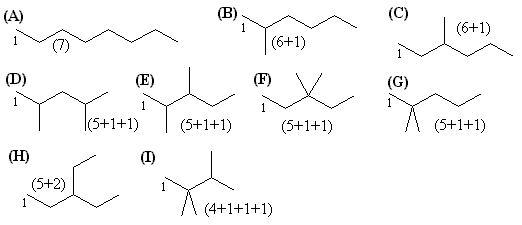
從以上結構可以推導出化學位移數值及吸收訊號的個數。結構(A)只會有四個吸收峰，因為碳一和碳七環境相同，碳二和碳六環境相同，碳三和碳五環境相同，題目中有七個不同的化學位移數據，因此(A)不符合。同樣的推理可消去(B)(D)(E)(F)(G)(H)(I)，只有(C)會有七個不同的碳譜訊號。要驗證這點，可用計算器試算一下，比較計算出來的化學位移值和實驗值相差多少。結果可參閱表二。

回歸實際面，由於儀器的進步，目前測碳十三光譜不但可知有幾個碳，還可以知道有幾種碳，由DEPT光譜圖可知各級碳的個數，故第三題可增加一個提示，列表如下：

38.98(CH2), 34.17(CH), 29.55(CH2), 20.18(CH2), 19.20(CH3), 14.40(CH3), 11.43(CH3)

數據顯示有一個CH，三個CH2，三個CH3，和上圖對照之後，結構中具有一個CH，三個CH2，三個CH3的分子只剩三個，即(B)、(C)以及(H)。觀察結構的對稱性，結構(C)會有七個碳譜訊號，(B)有兩個等價的甲基，應該只有六根碳譜訊號；(H)太對稱了，只可能有三根吸收峰。

從對稱性很順利地推導出第三題的解答是(C)，但您能指出每個訊號所對應的碳嗎？

首先，CH只有一個，最容易判定，因此34.17ppm這個吸收峰是三號碳的。

至於另外六根吸收峰，同樣是CH2，化學位移分佈從38.98到29.55到20.18，甲基訊號則是19.20到14.40到11.43，這都是因為環境不同而造成的。

3-甲基己烷(C)的三個CH2分別在碳二、碳四及碳五上，只看αβγ碳的個數的話，依續是(221)[碳二](231)[碳四]和(212)[碳五]，預估化學位移為31,40,22，由此可定出38.98是碳四的訊號，29.55是碳二的訊號，20.18為碳五的訊號。

至於碳一、碳六和3-甲基而言，預估值分別是11,13,20，故19.20是3-甲基訊號，14.40是碳六訊號，11.43為碳一訊號。

表二、3-甲基己烷各類型碳的分析結果


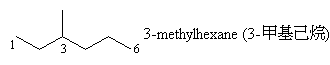變數	α	β	γ	δ	ε	１	２	３	４	預估	計算1	計算2	實際
碳一	1	1	2	1	1	0	1	0	0	11	11.4	10.87	11.43
碳二	2	2	1	1	0	1	0	1	0	31	29.8	29.60	29.55
碳三	3	2	1	0	0	1	2	0	0	40	33.7	34.59	34.17
碳四	2	3	1	0	0	0	1	1	0	40	38.9	39.10	38.98
碳五	2	1	2	1	0	1	1	0	0	20	20.4	19.96	20.18
碳六	1	1	1	2	1	0	1	0	0	13	14.2	14.35	14.40
3-Me	1	2	2	1	0	0	0	1	0	20	19.6	19.14	19.20

★結論

原則上，碳的級數愈高，化學位移愈大，從前面三個問題之中，我們看到二級碳的化學位移有可能大於三級碳者(比較3-甲基己烷的碳三和碳四)；相同級數的碳會因環境差異而有不同的化學位移(正庚烷的碳二碳三碳四)；利用αβγ三種碳的數目可以約略估計化學位移數值，對於結構鑑定有相當助益。

參考文獻

Silverstein, R. M.; Bassler, G. C.; Morrill, T. C.
Spectrometric Identification of Organic Compounds (5th. ed.),
John Wiley & Sons: NY, 1991, p235.
Becker, E. D.
High Resolution NMR: Theory and Chemical Applications (2nd. Ed.)
Academic Press: NY, 1980, p78.

2000, 10, 11.
<<上一篇｜回目錄｜下一篇>>